Crédit en espèces

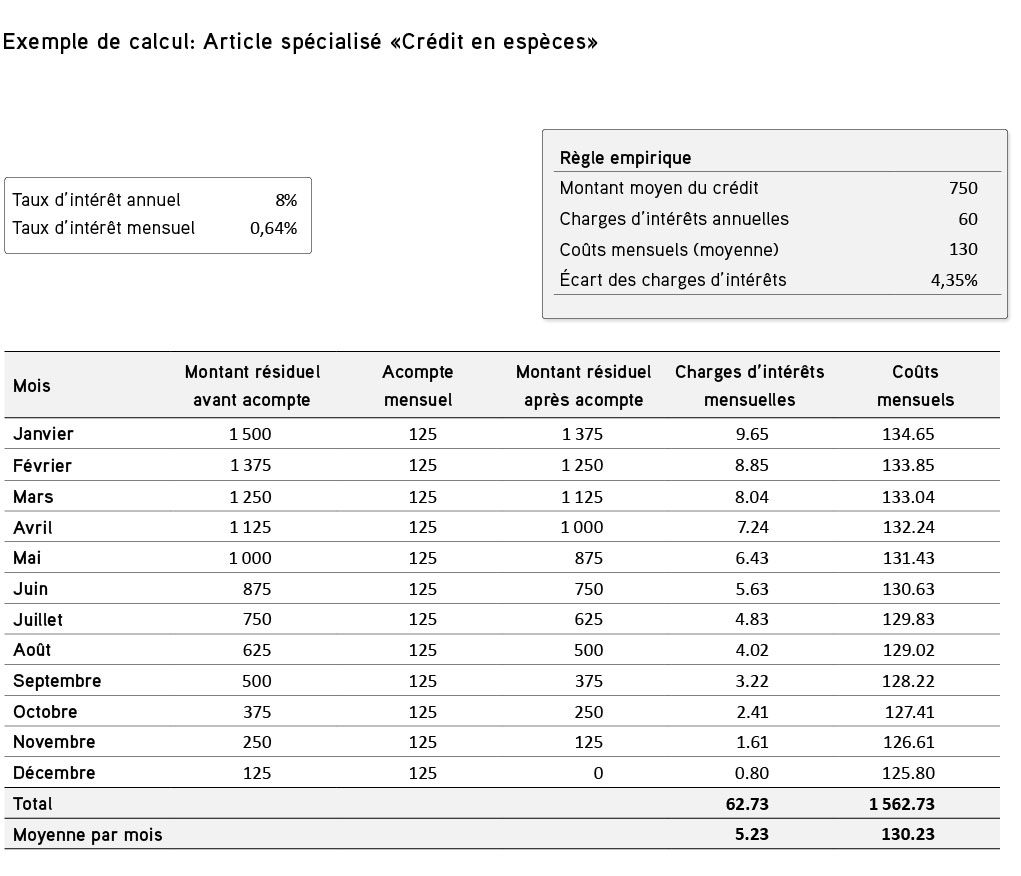
Le calcul des intérêts dans le module «Crédit en espèces» a été nettement simplifié pour les élèves. Cette fiche présente les différentes étapes des calculs à l’enseignant afin qu’il puisse mieux évaluer les connaissances à transmettre.

Le module est surtout axé sur le remboursement d’une dette augmentée des intérêts. L’amortissement prend la forme d’acomptes versés à échéances régulières. Cela signifie que le montant de la dette ne cesse de décroître entre la conclu-sion du contrat et son échéance, ceci à chaque fin de mois.
Dans le cas d’un crédit en espèces de 1500 francs d’une durée d’un an, le paiement par acompte s’élève à 125 francs par mois. Après 12 mois, la dette est remboursée.

Les intérêts versés sont le prix à payer pour l’argent prêté. Comme le montant dû s’amenuise au fil des mois, le montant des intérêts à payer diminue également. Puisque les intérêts doivent être réglés mensuellement, il faut commencer par convertir le taux d’intérêt annuel en un taux d’intérêt mensuel correspondant. Dans cet exemple, la banque propose le crédit à un taux annuel effectif de 8%.

D’après la formule ci-contre,un taux d’intérêt annuel effectif de 8% correspond à un taux d’intérêt mensuel de 0,64% envi-ron. Ce résultat nous permet maintenant de calculer les men-sualités dues par le débiteur. Pour ce faire, il faut calculer les intérêts mensuels dus sur le montant résiduel du crédit après déduction de l’acompte mensuel.

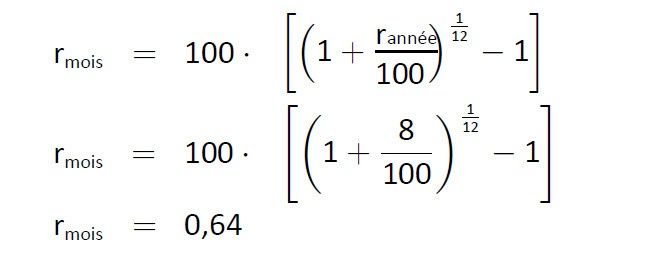
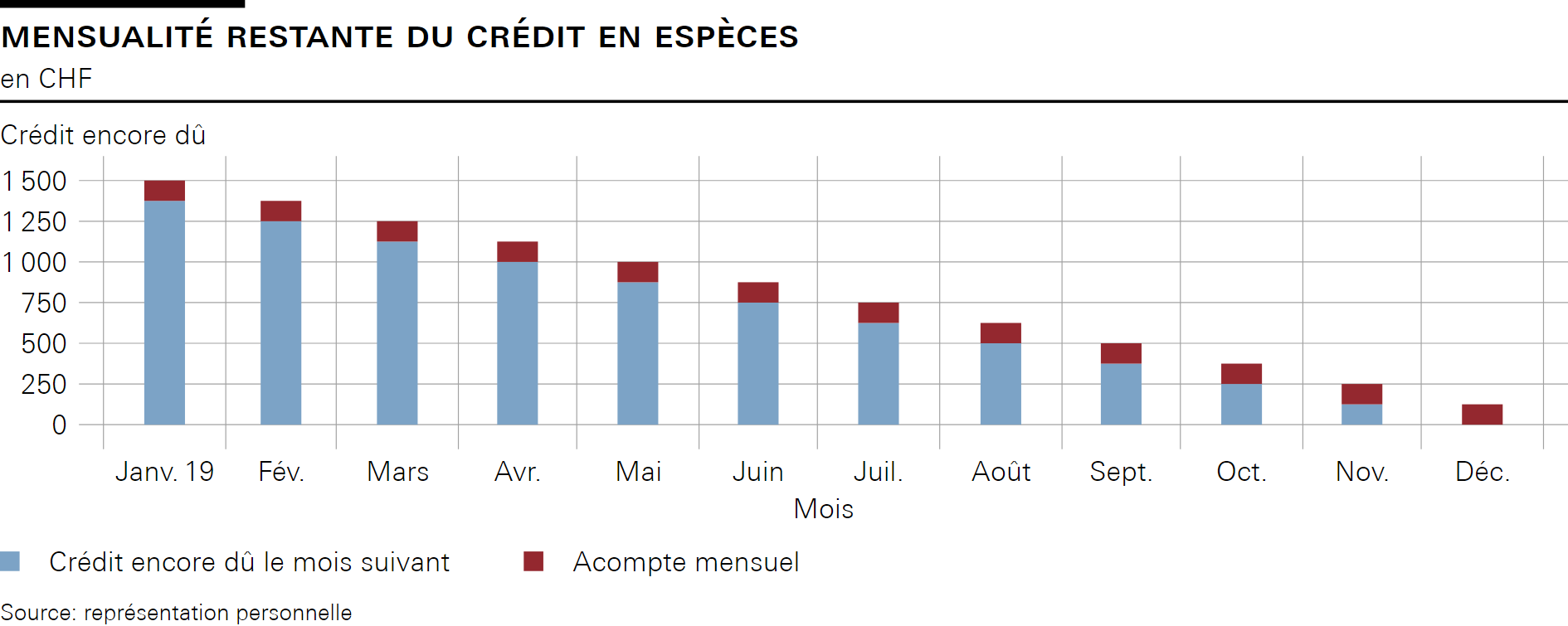
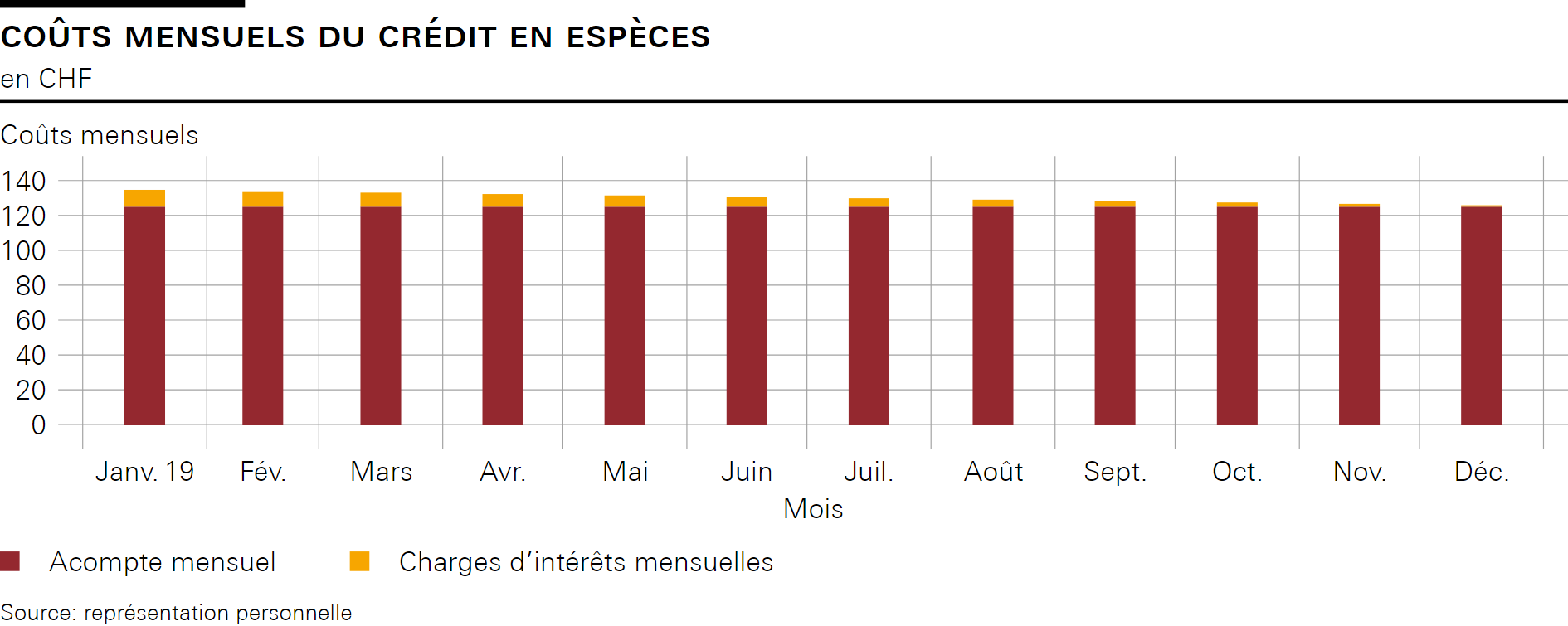
Dans le module «Crédit en espèces», le calcul simplifié des charges d’intérêts tient compte du fait que le montant total dû au titre du crédit (1500 francs) diminue progressivement au cours de l’année.
Dans notre exemple, le montant moyen dû s’élève à 130,23 francs environ (valeur médiane entre 125,80 et 134,70 francs). La règle de calcul empirique expliquée aux élèves dans l’article spécialisé donne 130 francs par mois. L’addition des intérêts s’élève à 62,73 francs. La règle de calcul empirique les évalue à 60 francs.

Deux explications pour cet écart entre les chiffres. Primo, le montant moyen résiduel du crédit s’élève à 812,50 francs et non à 750 francs. Toutefois, diviser en deux la somme du crédit est de loin un mode de calcul plus simple que de déterminer la moyenne effective (entre 1500 francs et 125 francs). Secundo, l’application du taux d’intérêt annuel surestime légèrement les charges d’intérêts.
Comme ces deux distorsions s’annulent, la règle empirique offre de bons résultats tout en simplifiant énormément les calculs. Dans notre exemple, l’écart est de 4,35% environ. Par conséquent, la règle empirique sous-estime légèrement les charges d’intérêts.